게임 수학 이란!
크게 3가지로 나눌 수 있다.
공간에 대한 수학 :
현실세계 vs 가상세계(게임 속 세계)
- 컴퓨터로 만든 가상 세계는 수로부터 만든 명확한 시스템. == 벡터공간(게임이 사용하는 가상공간의 본질)
- 물리학의 벡터(크기와 방향을 가진 대상)와 스칼라(크기만 있는 물리량)
- 수학에서의 벡터(벡터공간의 원소)와 스칼라(체 집합의 원소)
- 가상세계가 구축되는 원리를 파악해보자면 우리가 원하는 모습으로 가상세계를 변형해야 되는데 이것을 수학에서는 변환이라 한다(Transformation). 1초에 60프레임을 찍어내는 게임에서는 변환을 빠르고 단순하고 명료하게 이루어져야 한다. 이것을 선형 변환(Linear Transformation)이라 한다.
- 보다 그럴듯한 모습을 화면을 보여주기 위해 나름의 공간변환체제를 만들어 둔게 렌더링 파이프라인.
- 렌더링 파이프 라인 : 로컬공간 >>(모델링 변환) >> 월드공간 >> (뷰변환) >> 뷰공간 >>(원근 투영 변환)>> 사영공간
- 이러한 체계가 만들어 졌으니 컴퓨터에 일을 시켜야 하는데 이 일을 지시하기 위한 도구가 바로 수학의 행렬.((Matrix) - 선형 변환을 수행하는 도구)
- 행렬이란? 컴퓨터로 하여금 가상공간을 빠르게 변환시키도록 지시하는 일종의 명령어라 할 수 있음. 렌더링 파이프라인이 만들어져있는 만큼 행렬도 사용하는 행렬이 정해져 있지만 스스로 행렬을 설계할 수 있도록 기본원리를 이해하는 것이 중요함.
- 이것들을 이해하고 나면 다음으로 평면의 방정식을 사용해서 여러 개의 평면을 사용해서 자신의 공간을 구축하는 방법을 알아야 된다. >> 카메라가 보는 영역 == 절두체(Frustum) - 6개의 평면으로 구성. 게임의 특징인 보이는 물체만 걸러내서 렌더링 하는 수학적인 메커니즘이 만들어 지게됨. 이렇게 해서 1초에 60프레임이라는 빠른 렌더링이 가능하게 된 것.
- 가장 중요한 것 : 1) 수의 체계와 벡터 공간. 2) 선형 변환과 행렬
물체에 대한 수학 :
- 게임에서 사용하는 가상공간의 체계와 물체를 구성하는 데 사용하는 수학
- 가상세계는 다차원으로 구성된 수의 데이터인 벡터 공간으로 구성되어 있다 하였는데 벡터공간은 어떤 대상의 성질을 표현하는 데 사용되는 데이터. 따라서 벡터 공간의 공간과 현실세계의 공간은 다른 공간. 하지만 벡터공간으로 현실세계의 공간을 만들어 내야 한다. >> 공간의 차원을 늘린다. ex>> 2차원 물체의 표현- 2차원 , 이동의 구현 - 1차원 == 총 3차원의 공간을 활용, 3차원의 물체를 이동하려면 - 3차원의 물체의 표현 -3차원, 이동의 구현 -1차원 == 총 4차원의 공간을 활용.
- 수학의 벡터는 게임을 구현하기 위해 점 또는 (이동)벡터 중 하나로 사용된다.
- 게임은 벡터 공간을 1) 물체를 표현하는 공간 = 아핀공간 2) 이동을 위한 공간으로 분리해 관리한다.
- 아핀공간에 속한 요소들이 벡터이긴 하지만 이 요소들은 물체를 표현하는데 사용되고, 이 요소들을 구분 짓기 위해 별도로 점이라 하고, 따라서 가상공간의 물체는 점으로 구성되어 있다.
- 벡터공간의 다른 부분 공간인 이동을 위한 공간에 속한 벡터 == 벡터(Vector) 또는 이동벡터
- 수학적 벡터 : 벡터 공간의 원소. / 물리적 벡터 : 크기와 방향을 가진 대상. >> 이동벡터는 물리적 벡터에 해당.
- 아핀공간의 점을 사용해서 물체를 만들면 이물체는 이동벡터가 가지고 있는 크기와 방향을 사용해서 이 점을 이동시키도록 구현되어 있다.(점 --->점 , 화살표 = 이동벡터) 수식: P1 + v = P2 , 두 점 사이에는 하나의 벡터가 대응된다. v = P2-P1 (= 이동벡터를 알 수 있음)
- 정리하면, 게임은 벡터 공간을 1. 물체를 표현하는 공간. 2. 이동을 위한 공간.으로 분리하여 관리한다.
- 게임에서 보이는 3차원 공간은 실제로는 4차원 공간
- 게임공간 (움직일 일이 없기에 1차원(0,0,0)은 기본값으로 두고 3차원만 사용) = 월드공간
- 물체를 배치하는 과정 >> 물체의 공간(아핀공간의 점들로 구성되어 있음, 이 역시 4차원 공간으로 구성되어있음(물체는 이동을 하기에 1차원공간 적극적으로 사용 ) ) = 로컬공간
- 월드공간으로 로컬 공간과 점을 들고 겹쳐두는 거라 생각해야돼.
- 정리하면 >> 4차원 공간을 생성하고, 3차원 공간으로 대상을 표현하고 확장한 1차원 공간으로 이동을 구현. 벡터는 용도에 따라서 물체를 구성하는 데 사용하는 점과, 물체를 이동하는 데 사용하는 (이동)벡터로 나누어진다. 그래서 우린 점에 대한 수학과 이동벡터를 다루는 수학으로 나누어 공부할 거임.
- <게임을 만들기 위해서는>
- - 로컬 공간 : 개별 물체의 공간 (모델링 진행, 모델링한 결과물은 메시데이터로 변환되어 게임 엔진에 들어감. 게임엔진에서 메시 데이터는 세 개의 정점으로 구성된 삼각형으로 분해됨)
- - 월드 공간 : 물체들이 모인 게임의 공간.(우리가 흔히 게임 스테이지라고 부르는 공간)
- - 카메라 공간 : 플레이어가 보는 공간
- - 최종 렌더링 진행
- 게임이 시작되면 프레임마다 월드 공간이 사용자 입력과 지정된 로직에 따라 시뮬레이션되고(로컬공간 - 월드 공간의 변환) 이 프레임에 수행할 시뮬레이션이 완성되면 카메라에 보여지는 물체만 걸러내서 렌더링을 진행하게 됨.(월드 공간 - 카메라 공간의 변환)
- 전자를 게임 로직( :물체의 배치 설정), 후자를 렌더링 로직(: 화면에 그릴 데이터 설정)이라 말한다. 앞서 설명한 공간에 대한 수학과 점에 대한 수학은 렌더링 로직에서 굉장히 중요하게 사용됨.
-
- 게임 로직 단계에서는 특수한 경우를 제외하고는 점에 대한 수학을 쓸 일이 별로 없음. 게임에서 물체가 이동하는 것은 물체를 구성하는 점이 이동하는 것이 아니고 물체를 담는 공간이 이동하는 것(벡터의 수학). 따라서 이때는 점을 다루지 않고 평행이동한 공간의 원점과 그 공간을 구성하는 중심축의 변환에 대해서만 신경 쓰면 됨.
-
- 이렇게 공간의 변환을 설정하는 것을 트랜스폼이라 함.>> 트랜스폼(Transform) : 크기, 회전, 위치를 순서대로 조합한 변환. 트랜스폼의 최종 정보는 내부적으로는 행렬로 구성되어 있지만 게임 로직에서는 행렬의 정보를 사용하지 않고 크기, 위치, 회전의 3가지 데이터로 쪼개서 관리.
- 벡터에 대한 수학이란, 개별 물체가 가지고 있는 크기, 위치, 회전에 대한 정보를 계산하는 데 사용하는 수학을 말함. 벡터의 연산을 통해 벡터와 스칼라가 상호 순환하는 시스템이 만들어진다.
<벡터의 연산>
-
-
- 벡터와 벡터의 덧셈(기본) - 각축의 크기만큼 평행 이동
- 벡터와 스칼라의 곱셈(기본) -벡터가 가지고 있는 고유한 성질, 평면의 기울기로 볼 수 있음. 그 기울기를 그대로 유지한 상태에서 원점으로부터 크기를 쭉 조절해 주는 동작. ** 2의 스칼라의 짧은 정의: 사칙 연산이 가능한 수 집합의 원소를 의미( == 우리가 일상생활에서 사용하는 실수가 바로 스칼라)
- 벡터의 내적(응용)
- 벡터의 외적(응용)
-
-
- 1,2의 연산을 벡터의 기본연산이라 하는데 이 두 개의 연산을 조합해서 사용하면 새로운 벡터를 생성할 수 있다. 이것을 선형 조합이라 하는데 평행하지 않은 두 벡터를 조합하면 평면에 있는 모든 벡터를 생성할 수 있다.( == 평면의 경우, 평행하지 않은 두 기저 벡터를 선형조합하면 평면상의 모든 벡터를 생성할 수 있다.)
-
- 벡터의 두 기본 연산은 벡터의 생성 시스템에 사용하는 선형 조합을 구성하는 필수 연산임. 조합하는 데 사용하는 가장 기본적인 벡터 두 가지. >> x축에 해당하는 1.0과 y축에 해당하는 0,1 이 둘을 조합하면 공간에 속한 모든 벡터를 손쉽게 생성해 낼 수 있음. 이 두 가지를 표준 기저벡터라 부름.
-
-
- 표준 기저벡터(Standard Basis Vector) : 평면의 모든 벡터를 생성할 수 있는 기저(Basis)에서 가장 기본적인 기저벡터.
- 벡터를 다양하게 응용할 수 있는 별도의 연산이 바로 내적과 외적. 벡터의 내적과 외적은 게임 제작과정에서 벡터를 응용하는 데 사용하는 유용한 연산들이다.
-
-
-
- 벡터의 내적 (백터 응용에 관련된 거의 대부분의 공식에 들어감.)
- 벡터의 내적을 사용하면 두 벡터가 서로 직교하고 있는지 아니면 물체가 나의 앞쪽에 있는지 뒤쪽에 있는지 판별 가능, 어떤 시야각이 주어졌을 때 해당 시야각의 영역 안에 물체가 들어와 있는지 밖에 있는 지를 판단 할 수 있음.
- 어떤 벡터를 다른 벡터에 투영시킬 때 주요 사용. 내적의 투영 공식에서부터 평면에 방정식이 유도되고 이 평면들이 모여 절두체 영역(카메라가 보여지는 영역)을 만든다. 여기서 그 카메라가 보는 영역 안에 있는 물체만 골라낼 수 있는 수학공식과 알고리즘이 만들어짐.
- 벡터의 외적 (벡터의 외적연산은 3차원에서만 가능)
- 내적이 직교성을 판별하는 데 사용했다면 외적은 평행성을 판별하는 데 사용.
- 내적은 앞뒤를 판별하는데 사용한다면, 외적은 좌우를 판별하는데 사용.
- 벡터의 외적은 내적의 부족한 부분을 보충해 주는 성질이 있음. (상호 보완적인 성질)
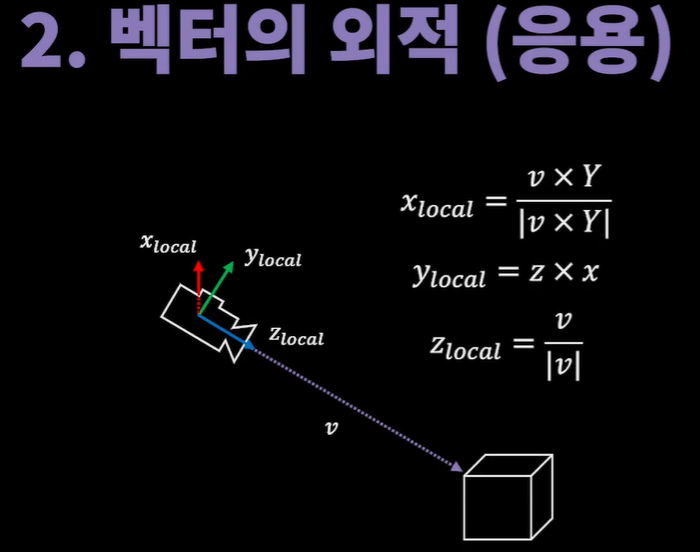
- 평행하지 않은 두 벡터의 조합은 평면을 만든다면, 여기에 수직인 벡터, 즉 평면의 방향을 외적을 통해서 파악할 수 있음. >> 이러한 과정을 계속 거치면 3차원 공간을 구성하는 세 가지 축을 모두 다 외적을 사용해서 계산할 수 있음.
- 벡터의 내적 (백터 응용에 관련된 거의 대부분의 공식에 들어감.)
-
3. 회전에 대한 수학
회전에 대한 수학 (삼각함수와 회전 행렬)
- 게임에서 변환은 물체가 움직이는 것이 아니고 물체를 담은 공간이 움직인다.
- 벡터공간을 집이라 하면 이를 떠 받들고 있는 주춧돌로 표준기저벡터(평면의 모든 벡터를 생성할 수 있는 기저에서 가장 기본적인 기저벡터)를 설명할 수 있다. 벡터공간의 모든 벡터는 표준기저벡터의 선형조합으로 만들어지기 때문.
- 표준기저 벡터를 변경시키면 어떻게 될까??
- 벡터 공간에 속한 모든 원소들이 표준기저벡터가 변화된 그 모습에 따라 모두 재배치 >> 공간 변환의 원리(>> 원 공간을 떠 받들고 있었던 표준기저벡터터를 변경시켜 새로운 공간을 창조하는 작업.)
- 회전 변환의 원리
- 회전 변환을 적용해 변환된 물체는 외형이 변하지 않는다.
- 표준기저벡터가 가지고 있던 성질을 그대로 유지시켜 변환시켜준다.
- 2차원 공간에서 크기가 1인 두 표준기저벡터가 가지는 (직교하는(직각)) 성질을 유지시켜주면 회전 변환을 만들 수 있음.
- 삼각함수 :
- 빗변, 높이, 밑변을 가진 삼각형 - 세 가지를 조합해서 만든 비를 삼각비라 한다. (높이/빗변, 밑변/빗변, 높이/밑변 >> 여기서 파생된 것이 삼각함수 : 높이/빗변을 싸인 함수, 밑변/빗변을 코사인 함수, 높이/밑변을 탄젠트함수라 한다.)

- 2차원 평면의 회전 행렬(Rotation Matrix)-- [ cos -sin ]- sin cos- 첫 번째 기저벡터가 변화된 값 두 번째 기저벡터가 변화된 값]
- 3차원 공간에서의 회전은 더 까다로움.
- 축- 각 회전 : 대표적인 방식 : 로드리게스 회전공식 >> 단점 : 행렬로 변환하기 어렵기 때문에 렌더링 파이프 라인의 중간에 위치힌 파이프라인 흐름이 끊기게 됨.
- 오일러 각 회전 (x, y, z 표준기저벡터를 총 세 번 돌려주는 방식) : 직관적이기 때문에 대부분의 3차원 그래픽 툴에서 사용하며 적은 양의 데이터로 3차원 회전을 표현할 수 있다. >> 단점: 한 번의 회전을 3번으로 끊어서 표현하기에 임의의 축에 대해 부드럽게 움직이는 회전을 계산하기 어려움(매움직임마다 3번씩 끊어서 회전하기 때문), 가끔 한 축의 회전이 증발해 버리는 짐벌락현상이 발생하기도 함.
- >> 3차원 회전을 안정적으로 구현하기 위해 다차원의 수체계를 사용해서 해결 >> 사원수(쿼터니언)
쿼터니언(사원수에 대해)
사원수(Quaternion) - 네 개의 원소(하나의 실수와 3개의 허수)로 구성된 수
실수 : a
사원수 : a + bi + cj + dk
수란 무엇인가 : 집합의 개념에서 수를 관리하고 있음.(집합이란 원소의 묶음을 의미) 수에는 연산이 존재하기 때문에 단순 집합과 차별점을 가진다. 수는 구조(시스템)를 가진 집합이다.
연산에 대한 공리(Axiom)
- 교환 법칙
- 결합 법칙
- 분배 법칙
- 항등원
- 역원
덧셈과 곱셈 연산에 대해 위 공리를 가지는 집합은 수가 될 수 있다.
복소수 - 두 개의 원소로 구성된 수 a + bi
사원수 - 실수부와 허수부로 구성
모든 회전이란 크기가 1인 수와의 곱이다.
크기가 1인 복소수의 곱은 평면에서의 회전 변환과 동일하다.
크기가 1인 사원수와의 곱은 4차원 공간에서의 회전을 의미한다.
사원수의 활용
- 사원수를 사용해 빠르게 벡터를 회전시킬 수 있다.
- 축-각 방식이고 절반의 각으로 파생되기 때문에 일반인들이 직관적으로 사용하기는 어렵다.
- 게임 제작에서 고정된 각을 지정하기 위해서는 오일러 각은 여전히 유용하다.
- 사원수는 행렬로 변환이 용이.
쿼터니언과 오일러는 인프런 강의로는 제대로 이해되지 않았다.
자세하게 나온 블로그 참고 : https://luv-n-interest.tistory.com/805
728x90
반응형
'게임' 카테고리의 다른 글
| 게임+유니티 ) pseudo 3D game에 대해 들어봤는가.(feat. 고전 게임 outrun) (3) | 2024.11.25 |
|---|---|
| VR ) XR Interaction ToolKit개념과 핵심 기능 2 (1) | 2024.01.02 |
| VR ) XR Interaction ToolKit개념과 핵심 기능 1 (0) | 2023.12.28 |
